Who was Baudhayana?
Not much is known about Baudhayana. However, historians attach the date c. 800 BCE (or BC). Not even the exact date of death of this great mathematician is recorded. Some believe that he was not just a mathematician but in fact, he was also a priest and an architect of very high standards.
he case of Baudhayana is one of the many examples where Greeks and other western civilizations took credit of the discoveries originally made by ancient Indians. Baudhayana in particular is the person who contributed three important things towards the advancements of mathematics:
He gave us the theorem that became known as Pythagorean Theorem. Actually we should be calling it Baudhayana Theorem.
He gave us the method of circling a square.
He also gave us the method of finding the square root of 2.
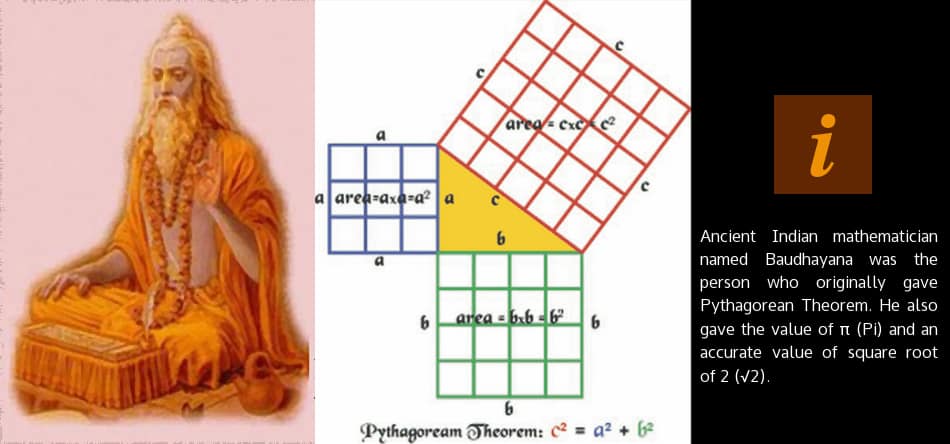
The Pythagorean (Baudhayana) Theorem
Baudhayana wrote what is known as Baudhayana Sulbasutra. It is one of the earliest Sulba Sutras written. Now Sulba Sutras are nothing but appendices to famous Vedas and primarily dealt with rules of altar construction. In Baudhayana Sulbasutra, there are several mathematical formulae or results that told how to precisely construct an altar. In essence, Baudhayana Sulbasutra was more like a pocket dictionary, full of formulae and results for quick references. Baudhayana essentially belonged to Yajurveda school and hence, most of his work on mathematics was primarily for ensuring that all sacrificial rituals were performed accurately.
One of the most important contributions by Baudhayana was the theorem that has been credited to Greek mathematician Pythagoras. There is an irony to this as well that we will discuss in a while.
Baudhayana’s Contribution towards Circling a Square and Pi
It was not just the Pythagorean Baudhayana Theorem that was first provided by Baudhayana. He even gave us the value of Pi (π). The Baudhayana Sulbasutra has several approximations of π that Baudhayana possibly used while constructing circular shapes.
The various approximations of π that can be found in Baudhyana Sulbasutra are:
$$\Pi =\frac { 676 }{ 225 } =3.004$$
$$\Pi =\frac { 900 }{ 289 } =3.114$$
$$\Pi =\frac { 1156 }{ 408 } =3.202$$
None of the values of π mentioned in Baudhayana Sulbasutra are accurate because the value of π is approximately 3.14159. However, the approximations that Baudhayana used wouldn’t really lead to major error during the construction of circular shapes in altars.
Baudhayana’s Contribution Towards the Square Root of 2
Interestingly Baudhayana did come up with a very accurate value of the square root of 2, which is denoted by √2. This value can be found in Baudhayana Sulbasutra Chapter 1, Verse 61. Whatever Baudhayana wrote in Sanskrit actually boils down to this symbolic representation:
$$\sqrt { 2 } =1+\frac { 1 }{ 3 } +\frac { 1 }{ \left( 3\times 4 \right) } -\frac { 1 }{ \left( 3\times 4\times 34 \right) } =\frac { 577 }{ 408 } =1.414215686$$
This value is accurate to 5 decimal places.
In case Baudhayana restricted his approximation of √2 to the following:
$$\sqrt { 2 } =1+\frac { 1 }{ 3 } +\frac { 1 }{ \left( 3\times 4 \right) }$$
In above restricted case, the error would be of the order of 0.002. This value is way more accurate than the approximations of π he provided. This is where one confusing question pops up – “why did Baudhayana need a far more accurate approximation in case of √2 compared to π?” Well, there is no one who can give us that answer.
Bottom line however is that it was Baudhayana who gave us the Pythagorean Theorem, the value of π and the square root of 2. The Greeks and other western mathematicians simply stole those discoveries, who, through the annals of history, became known as the discoverers of those concepts while Baudhayana remained discredited for his discoveries that laid down the foundations of geometry and algebra.

